10.2 Environment Lighting
在前面的章节中有提到一个简单的单光源的光照模型。但在现实中我们还需要考虑到环境反射的光对我们物体的影响。不过环境光照这里本身主要还是讨论的一个局部光照的情况,也就是说我们所谓的 环境 并不是场景中渲染的其他物体,那会在全局光照中讲到。环境光照环节的环境光主要是来自于渲染的物体们之外的 背景。
一个非常简单的环境光的模型就是Ambient light, 考虑的是整个环境的光强以及颜色都是一个相同的值 LA:
\[L_o(v)=\frac{\rho}{\pi}L_A\int_{l\in \Omega} (n \cdot l)dl\\ =\rho*L_A\]因为我们只考虑同一个光强,因此计算上也特别的简单,如果是用的兰伯特漫反射的模型就会像上面那样去计算。当然如果需要用到其他的
BRDF 也不会特别的麻烦:
\[L_o(v)=L_A\int_{l\in \Omega} f(l,v) (n \cdot l)dl\\\]10.3 Spherical and Hemispherical Functions
要得到更进一步的渲染效果,我们会希望说环境光是更加复杂的一个情况,而不是一个常数的 Ambient 。 也就是说来自不同方向的光应该会根据场景需要拥有不同的值,我们可以把这个性质称作 球面函数,代表球心往球面的每个方向拥有不同的光照值。 我们要做的其实是根据某种 球面函数 把光源信息投影到任意的载体上,然后在渲染过程中去读取那个载体。
10.3.1 Simple Tabulated Forms
最简单的投影球面函数的方式就是直接把固定数量的采样方向的值存起来。 例如我们使用一个矩阵,然后每个格子都存其中一个方向的光照值。更简单的理解就是把球面函数的值储存到一个 2D纹理 上面。
这种说法是非常好理解的,不过我们的卷积计算会非常的难办。大部分时候由于我们的光照计算需要算一个半球内的光照值,如果储存成这样的格式我们很难去进行大范围的光照查找。还有一点就是这种储存形式并不是旋转不可变,也就是说如果我们希望场景光照旋转,这个方式很难达到理想的效果。同时储存的精度也会对结果造成不小的影响。
一个比较常见的例子Ambient Cube,使用六个纹理元素来储存环境光照信息。相当于是使用一个立方体,然后每一面是一个光照颜色。我们实际的环境光照的时候会根据选择方向最近的三个面的插值去计算。这个手法本身在投影以及读书数据时是非常方便的, 更重要的是重建( 例如让环境光旋转 )的开销也会更低。
10.3.2 Spherical Bases
除了把结果储存到一个纹理上以外,我们也希望能用更少的储存去重建整个 球面函数。 可以的话希望用尽量少的参数来重建,也就是使用含有固定参数的函数来重建整个球面情况。这时候被引入的概念就是基函数。
很多时候我们没办法单纯的用一个简单的函数去重建一个复杂的函数,不过我们如果有很多的简单函数,是可以做到近似原本的复杂函数的情况的。比如说下图,我们使用了四个简单的曲线函数来对原本的函数进行了一定程度上的重建:

在后面的笔记里我会把这种简单的函数称作 基函数 。
10.3.2.1 Spherical Radial Basis Function
上面提到的重建例子是一个 2D 的情况, 放到 3D 的球面被提出的就是 SRBF(Spherical radial Basis Function), 他的性质是径向对称性,所以对于这种类型的基函数我们只需要提供一个参数即可。
对于一个球面来说,我们则需要均匀的分配大量的基函数覆盖球面,每一个覆盖的区域都是一个 lobe。 在重建整体光照的时候也只需要展开所有的 lobe 去计算就可以了,具体还是看使用了多少个 lobe 。
10.3.2.2 Spherical Gaussian
这是 SRBF 的其中一种实现,对于一个 lobe 使用下面的函数来形容:
\[G(v,d,\lambda) = e^{\lambda(v\cdot d-1)}\\ v: 采样方向\\ d: lobe中心方向\\ \lambda: 控制形状的参数\]我们在计算特定方向的光照的时候可以直接展开一定数量的 lobe 去计算。而这个表达式本身也支持很多方便与采样上的操作:
例如如果我们要计算两个 lobe 在一个方向上的值:
\[G_1G_2 = G(v,\frac{d'}{||d'||},\lambda ')\\ d' = \frac{\lambda_1d_1 + \lambda_2d_2}{\lambda_1+\lambda_2}\\ \lambda'=(\lambda_1 + \lambda_2)||d'||\]并且对于单个lobe 于球面的积分也是很好算的:
\[\int_\Omega G(v)dv=2\pi \frac{1-e^{2\lambda}}{\lambda}\]这两个性质能够带来什么?如果我们要在计算光照的时候考虑一定范围内的光源的总合,那么我们完全可以选取一定范围内的 SG lobe, 把他们通过第一个公式叠加在一起,然后当作单个 lobe 算积分。
10.3.2.3 Spherical Harmonics
SH 方法是使用了一组的正交基来对我们的球面函数进行重建。 所谓正交基也是一组的基函数,不过有一个特殊的性质就是基函数于基函数之间是保持正交的。正交代表着基函数与基函数之间的内积为零, 简单点来说就是函数之间拥有不可替代性。你不能用其他基函数的权值来替代任何一个基函数的贡献值。例如我们拿下面的图来说,每一个基函数之间都是没有内积的,贡献不重叠:

正交基的限制可以带来在投影上面的方便性。也就是说当我们要把整个 球面函数 写到不同的正交基上面时,过程会非常的暴力且方便。由于我们正交基之间没有内积,那么我们完全可以理解成 球面函数 在一个正交基的范围内,与那个正交基的内积结果就会是那个正交基的权值。
\[定义:\\ k_j= <f_{target}(),f_j()>\\ f_{target}() \approx \sum^n_{j=1}k_jf_j() \\ 变量:\\ f_{target}: 整体球面函数\\ f_j: 正交基函数 \\ k_j: 正交基权值\]由于这个特性,我们可以很好的去计算出每个固定的正交基所拥有的权值,所以投影和读取光照的值会变得很方便。还有一个优势在于他是旋转不变的,也就是说我们可以很方便的去旋转我们的光源。关于 SH 最经典的是下面的图:
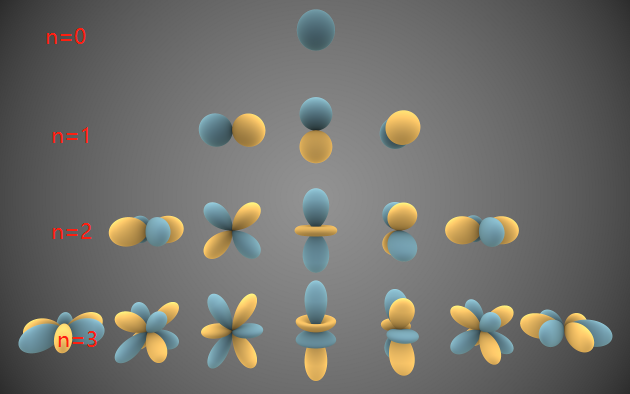
图里的球代表的就是三维情况的值,蓝色为正,黄色为负。从上到下每一排为一阶,使用的阶级越高,那么我们对 球面函数 的还原更加的精准。具体的使用方法就是为图里的每一个形状加一个权值,然后把所有的结果加在一起,就可以还原出来了。
一般来说我们会使用到二阶的 SH, 也就是使用了九个正交基。那么这时候我们就只需要提前算好九个权值,并且记录下来就可以把整个场景的光照的近似给储存起来。相较于其他方法来说,储存上的要求是十分低的。
10.3.3 Hemispherical Bases
上面提到的方法都是要复原整个球体光照后取半圆范围内的光照信息来计算。这相当于对每一个需要光源的像素我们都多重建了一个无效的半球信息。因此被提出的方法是 Hemispherical Bases, 就是只需要复原半球方向的信息的做法。
10.3.3.1 Ambient/Highlight/Direction
这里并没有对这个方法解释的很清楚,大致上就是对于每个方向,储存了一个方向,高光,以及环境光。个人理解是类似于 Simple Tabulated Forms 的储存方式,只是每一个格子不止有这个方向的直接光照,而且还附带了这个方向为中心的环境光。
实际上作用就是比起单纯的多重采样整个环境光的情况,我们可以通过单次采样来得到半球的光照信息。
10.3.3.2 Radiosity Normal Mapping
这是 半条命2 使用的一个方法,很多的光照的表达方式都是基于储存我们法线方向的光。也就是说我们用一个光照纹理,来储存法线上面的的光照信息,或者说法线为中心方向的半球信息。
这个做法采取了不同的思路,比起使用单个光照纹理,这里使用的是三个纹理。我们可以在一个切线空间上除了法线之外,生成三个正交向量,而这三个正交向量就是这个计算方式的核心,具体向量方向如下:

我们比起为每个方向的 n 生成光照图, 在这里我们会为三个正交向量的方向各自生成一个光照图。 对于每个光照图来说,具体的物理意义是:在平面的法线为n时,来自方向m的光照值为多少。
三个光照贴图对于每个点来说,就可以得到每个点的平面来自三个正交方向的光照值,并且对他们进行一定的插值就可以近似的得到这个 像素/平面 的半球环境光照值。插值的方法采取的是使用法线方向和这些正交向量的点乘,这样可以配合法线贴图来得到更好的一个视觉效果。
事实上这里其实只是提到一个概念,并没有说是要用三张纹理来实践…整体思路是记录三种光照信息,不过个人感觉应该用纹理比较妥当。
10.4 Environment Mapping
直到这个地方这本书才终于提到 Environment Mapping。 个人感觉从 Simple Tabulated Forms 哪里就很适合引出这个题目了。 环境贴图呢就是使用纹理作为载体来储存我们的 球面函数。我们只需要用一张贴图去储存所有法线方向的光照内容就可以了。
上面有些部分的内容并没有特别的去提到一个实践的方式,比如说Ambient/Height/Direction 和 Radiosity Normal Mapping, 因为提到的只是思路而不是具体实现,甚至可以是针对特定物体的局部信息去进行预计算的。
我们同时也会把环境贴图这样的技术叫做 IBL (Image-based Lighting) ,很多时候会使用现实生活中的全景图去当作一个环境光照的信息。
10.4.1 Latitude-Longitude Mapping
把环境光照信息储存在一个平面的纹理上,坐标为纬度和经度。不过这导致我们在计算的时候需要根据我们的方向坐标去计算出这两个值,并且会需要用到 arccos / atan 这些开销较大的函数。
10.4.2 Sphere Mapping
球面映射则是使用类似于上面的映射但计算更简单的方式,如下。这里把 z方向的向量给映射到 [0,2]的区间,作用具体是让法线朝中间的待在地图的中间,背向我们的则靠外围。(右手坐标)
\[Given\ vector\ (r_x,r_y,r_z)\\ m=\sqrt{r_x^2+r_y^2+(r_z+1)^2}\\ u=\frac{r_x}{2m}+0.5\\ v=\frac{r_y}{2m}+0.5\]具体其实是把物体投影到半个球面上,如下(左边为经度纬度,右边为球面映射):

他的优势是储存要求没那么高,并且计算起来也很简单,因为不需要复杂的函数。不过同时也有一个很大的问题,就像图上面一样,我们最后生成出右边这样的图,中间部分非常的细节,靠外围就比较粗糙,因为这是基于目前的视角去生成的。
如果我们场景需要去转向摄像机,那么就需要重新生成一张图,这就是这个算法的问题所在。
10.4.3 Cube Mapping
这是现在最常见的方式了,使用一个六面的贴图形成一个方块来当作我们的环境光照的资源。这种做法是直接省去了计算转换的麻烦,因为我们的方向向量在GPU的支持下可以很顺利的得到其中一张贴图的其中一个纹理元素的值(或者插值)。

相较于球面映射来说,我们完全不需要在更新摄像机的时候去更新映射,因为这是独立于视角的。
10.5 Specular Image-Based Lighting
在前面提到环境映射的时候我一开始想的主要是用于计算我们的 BRDF 积分来代替常量的 Ambient 项。 不过似乎环境映射最开始是用来进行镜面反射的一个技术,也就是说我们使用环境贴图来对镜面物体着色。
不过并不是所有物体都是拥有平滑表面的,我们会有很多 Glossy 的材质,针对这些材质我们没办法说去根据反射去得到其中一个采样点来达到一个镜面的效果。所以我们可以对一个环境贴图进行模糊,模糊了后采样的就是一个更加粗糙的反射结果。
上面的这些部分是跟 BRDF 没有关系的,只是在一个非 PBR 的光照模型下去形容反射的情况。因为实际上我们的 BRDF 对于入射光的范围是比较讲究的。我们没有办法去进行一个统一的模糊,来让我们的环境贴图可以轻易的被所有材质的 BRDF 使用。 根据粗糙度金属度等参数我们完全可以得到不同的 lobe 分布,需要不同等级的模糊方式。 在最简单的情况下我们会只考虑非物理的反射以及粗糙反射,还不能拿来做 PBR。
10.5.1 Convolving the Environment Map
要做到一个更加真实的环境光照的效果,我们就需要为考虑到视线的每个角度的高光 lobe 去计算环境光照的值。我们目前使用纹理光照的情况下,是没有办法进行其他的积分计算,只能用加的,不过如果要把整个球的采样都算上那开销太大了。一般来说我们会考虑使用蒙特卡洛:
\[\int_\Omega D(l,v)L_i(l)dl \approx \frac{1}{N}\sum^N_{k=1}\frac{D(l_k,v),L_i(l_k)}{p(l_k,v)} \\ D:Specular\ lobe\\ p(l_k,v): PDF\ for\ L_i\]这里使用的 PDF 相当于是我们采样的方向的面积占整个求面积的百分比。之所以要除它就是用来假设我们所有方向的光照都跟目前采样的光照一致。之后再根据采样数量来做除法,就可以用少量的采样去模拟整个半球范围内的总合光照值。不过一般来说蒙特卡洛效果并不会很好,因为在很多的方向上我们会得到一个无效的采样,就是说我们采样的光源方向会根本不属于我们需要的 lobe 里面。
这里我们可以在蒙特卡洛之上采取重要性采样,就是说在我们选择蒙特卡洛的采样的时候,带入 lobe 的形状来做选取采样方向的概率分布。这样可以得到更有用的数据也可以采样稍微少一些方向。
无论如何这种手法考虑到视线是没有办法进行预计算的,但是在运行时去进行多重的采样是要尽量去避免的。
10.5.2 Split-Integral Approximation for Microfacet BRDF
用环境贴图来做 BRDF 高光的情况其实是很多的,想要把 Ambient 项去掉就得这样。上面提到的蒙塔卡罗就是一个办法,比如说我们可以用蒙特卡洛来进行下面的操作:
\[\int_\Omega f(l,v)L_i(l)(n\cdot l)dl \approx \frac{1}{N}\sum^N_{k=1}\frac{f(l,v)L_i(l_k)(n\cdot l_k)}{p(l_k,v)}\]不过这样的计算开销是很大的,即使算上重要性采样我们也需要采样很多的点才能得到一个理想的效果。所以这里被提出的方法 Split-Integral / Split-Sum 就是用近似的方式去预计算一些值,让我们可以在单次采样中得到像哟的结果。
实际的做法如下:
\[\int_\Omega f(l,v)L_i(l)(n\cdot l)dl \approx \int_\Omega D(r)L_i(l)(n \cdot l)dl \int_\Omega f(l,v)(n\cdot l)dl\]看起来这样的拆解是比较不数学的,但实际上为预计算值让我们可以单次采样到想要的结果,这样的近似是可以接受的,下面主要讲一下左右两个积分 (光照和材质) 具体要怎么预先计算:
光照
光照部分我看过两种不同的表达方式,一种是书里的一个是Games202 的:
\[书: \int_\Omega D(r)L_i(l)(n \cdot l)dl\\ 202: \int_{\Omega fr}L_i(l)dl\]这两个表达方式实际上是差不多的,主要代表着就是根据材质光源和视线所形成的 BRDF lobe 内部采样的光照总合。因为我们在不同的场景下会有不同的一个采光的范围,而不是直接对半球范围内去采样全额的光照。
这里的预计算方式也很简单(非常的近似), 就是我们生成好几个不同程度的卷积过的环境贴图。然后在我们Shader 实际运算的时候,会根据目前的材质算出一个 Lobe 大小来选择对应的环境贴图来采样光照。
简单来说就是先提前卷积好很多份环境纹理,之后根据需要去对范围相近的那个进行 单次采样。
材质
材质这里主要还是我们怎么去预先计算整个 Specular BRDF, 也就是:
\[f(l,v)=\frac{F(h,l)G_2(l,v,h)D(h)}{4(n\cdot l)(n\cdot v)}\\\]在常规的情况下,我们需要根据我们为蒙塔卡洛设置的采样数量 N 去计算 N 次不同的材质信息,因为我们要结合不同的材质信息,视角,光线角度等多维度的参数去计算不同的采样。具体算一下的话有下面几个参数要去考虑:
- 菲涅尔: F0、视线、光线、法线。
- 集合遮蔽: 粗糙度、视线、光线、法线
- 法线分布:粗糙度、视线、光线、法线
参数是非常多的,如果我们要为这些参数预计算一个 把积分算完 的纹理,是几乎不可能的,因为维度太高了。所以这里要做的就是把一些参数放到积分外面,或者把参数移除。
这里我们直接的就是做了几个假设,就 BRDF 来说有 视线=法线=反射, 并且使用的是 Phong 式的高光向量 (指不用半程向量,而是用光和反射光这两个向量)
\[f(l,n) = \frac{FGD}{4(n\cdot l)}\\ F:F(\theta) = F_0+(1-F_0)(1-(n\cdot l))^5\ 用冯氏把v\cdot h变n\cdot l\\ G: G=G_1(n\cdot n, roughness)G_2(n\cdot l, roughness )\\ D: D(roughness,n\cdot l)\]这样的做法里面带着一些小错误,我看Karis 的原文并没有处理法线分布,因为跟其他函数使用的角度不一样。不过在 Games202 中的处理是视为相同的角度来做近似。所以在这里我们把法线分布跟菲涅尔一样,把 V点H 换成了 N点L 。通过上面的操作,我们整个BRDF 就只剩下三个变量了:
- F0:积分时不变
- 粗糙度:积分时不变
- n点乘l:可以储存围绕一个中心的光线向量进行积分(预计算的积分中每次采样的l都是在中心光线的半圆范围内)
然后我们还可以继续提,可以把F0提到积分外面:
\[F(\theta) = F_0+(1-F_0)(1-(n\cdot l))^5\\ =F_0+(1-(n\cdot l))^5-F_0(1-(n\cdot l))^5\\ =F_0(1-(1-(n\cdot l))^5)+(1-(n\cdot l))^5\\ \\ \int_\Omega f(l,n)(n\cdot l)dl =F0\int_\Omega \frac{f(l,n)}{F}(1-(1-(n\cdot l))^5)(n\cdot l)dl+\int_\Omega \frac{f(l,n)}{F}(1-(n\cdot l))^5(n\cdot l)dl\]提到外面后,意思就是说F0 是不需要在积分内计算的,那么我们整个预计算的 BRDF 积分就只剩下粗糙度和 n点乘l 两个参数。那么我们可以预先为这两个参数生成一张预计算的贴图,预计算过程可以使用蒙特卡洛。不过要注意的是 环境 BRDF 这里要计算出两个不同的值,一个是左侧后来要乘以 F0 的值,一个是不用的。
计算时流程
这里采取的是 Karis 原文里面的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
float3 ApproximateSpecularIBL( float3 SpecularColor , float Roughness , float3 N, float3 V )
{
// 得到角度
float NoV = saturate( dot( N, V ) );
// 得到基于视角的反射向量
float3 R = 2 * dot( V, N ) * N - V;
// 根据R和粗糙度决定的lobe来查找对应的环境光图, 单次采样
float3 PrefilteredColor = PrefilterEnvMap( Roughness , R );
// 根据粗糙度和角度查找提前算好的材质数据
float2 EnvBRDF = IntegrateBRDF( Roughness , NoV );
// 这里直接相乘结果。 右部分为: F0*brdf.x + brdf.y
// 因为brdf这里预计算了两个通道,一个要乘F0一个不用
return PrefilteredColor * ( SpecularColor * EnvBRDF.x + EnvBRDF.y );
}
小总结
实际上无论是书上,Karis原文,还是Games202 都没有很深入的去讲部分细节的实现,可以理解为这是一个大体的实现框架,对 BRDF 内部采取的函数和具体参数也都是不一样的。很多的操作他并没有办法完全替代直接用蒙特卡洛多次采样的效果,毕竟我们这里只是去用一个近似的操作。
我在上面细节处理的地方主要是考虑了 Games202 和 Karis 的原文,他们一个抛弃了 几何遮蔽 **项,一个抛弃了法线分布,我觉得这人还是具体看想要实现的效果吧。书上也有提到高光角度这里不一定需要像 **Phong Shading 那样抛弃半程向量的效果,是可以用其他手法近似 Blinn Phong 的。
顺便一提这部分主要还是在计算一个高光,并没有考虑漫反射的部分。这里的环境光纹理为 高光环境光纹理 Specular Environment Map
10.6 Irradiance Environment Mapping

上面的地方我们更多是用环境贴图去形容一个镜面反射,或者是高光的情况。不过我们的渲染模型很多时候也会考虑到漫反射这一点。不同于高光的计算,漫反射需要的光照的数据并不包含法线分布、视角等影响,也就是说会跟材质没有任何的关系。所以比起像上面这样我们需要根据 lobe 的大小去生成不同程度模糊的环境贴图,我们这里只需要一张图,用来形容每个法线方向的 辐照度(辐射通量/面积) 。一般来说会像上图一样存在一个立方体纹理。
这时候我们并没有过多的对 lobe 范围考虑,因为一个面积所受到的光是基于它朝向的整个半球范围内的光,因此我们这里的环境贴图实际上就是每个点涵盖了以自己为中心的半球内的光照值(以及角度的权值修正n点乘l),我们可以在高光环境纹理的最模糊的 Mip Level 储存这个数据。
在使用这种图的情况下,我们不止可以用一个预先准备好的天空盒代表我们的漫反射环境光,我们甚至可以在运行时动态的加载新的光源。具体方法是以摄像机为中心朝着新光源的方向建立一个半球体。并且根据半球的几何数据区计算新的光源对光照图的贡献。
10.6.1 Spherical Harmoics Irradiance
之前提到过我们除了使用贴图,也可以使用 SH 来表达整体的一个光照情况。同时我们也可以使用 SH 来代表所有方向的辐照度。一般来说我们只需要用到二阶(九个参数,三个通道加起来为二十七个参数) 的 SH。
而且假设我们今天为场景的光照生成了一个常规的 SH, 我们就可以直接的通过让每个参数乘以固定常量来把光照 SH 编程 辐照度 SH,这个过程是十分的迅速的。唯一要注意的地方是我们的 SH 的参数不能有0, 就先在某一个正交基上我们不需要光照值也需要派给它一个非0的权值,在有的时候这样的操作可能会产生一定程度上的走样。
同时这个方法也支持动态的环境贴图。把动态的环境投影到一个 辐照度SH 并不会很困难,在动态的新增光源的情况下我们只需要把新增的系数叠加到原本的 SH系数 上面,而不需要复写之前的其他数据。
除了SH 外,也可以用其他方法表示辐照度,虽然用到的时候比较少:

从左到右为: 蒙塔卡洛+贴图,Ambient Cube, SH, Spherical Gaussians, H-basis
10.7 Source of Error
在着色的过程中我们肯定是需要对 非点光源 的光去进行积分,这在实践中需要用到特别多的近似的手法,因为目前来看我们去形容一个可积分的面积光的办法并没有特别的准确。在考虑到 BDRF 和光照模型的时候,因为我们使用了很多不同的手法去形容光照,整个渲染模型它并不是一个 整体 ,但我们也只能尽可能的让我们的 BRDF 可以确保不同形式的照明之间都可以共用。
我们也没有特别多的办法可以对 阴影/遮挡 进行更贴切的形容,因为很难去形容一个体积光的 体积。即便现在的渲染技术越来越发达,不过我们始终是在做近似的操作,他不一定是真实世界的物理效果。