4.1基本变换
Affine(仿射): 变换后保持线和线之间的平行性
Orthogonal(正交): 逆矩阵为转置后的矩阵
| 符号 | 名字 | 特点 |
|---|---|---|
| T(t) | 平移矩阵 | 移动一个点,仿射变换 |
| Rx(ρ) | 旋转矩阵 | 围绕x轴旋转ρ弧度。仿射变换&正交矩阵 |
| R | 旋转矩阵 | 仿射变换&正交矩阵 |
| S(s) | 缩放矩阵 | 仿射变换 |
| Hij(s) | 错切矩阵 | 仿射变换 |
| E(h,p,r) | 欧拉变换 | 使用欧拉角进行Pitch/Yaw/Roll旋转,仿射变换 |
| Po(s) | 正交投影 | 平行的投影物体到一个体积内,仿射变换 |
| Pp(s) | 透视投影 | 透视(不平行)的把物体投影到一个体积内 |
| slerp(q,r,t) | 球面线性插值变换 | 给出q和r基于t的四元数插值 |
4.1.1 平移
假设我们想要进行一个t的平移,定义为往x平移tx,y,z同理。那么我们需要把整个平移的变换写成下面的矩阵T的形式:
\[t = (t_x,t_y,t_z)\\ T(t) = T(t_x,t_y,t_z) = \left[ \matrix{ 1\ &0\ &0\ &t_x\ \\ 0\ &1\ &0\ &t_y\ \\ 0\ &0\ &1\ &t_z\ \\ 0\ &0\ &0\ &1\ } \right]\]这样我们的平移操作就会变成:
\[Vertex\ v = (0,0,0)\\ v' = T(t)·v\\ v' = (t_x,t_y,t_z)\]上面这样操作的前提是我们的顶点的坐标采用的是列优先的表达式,也就是说一个向量是以一个列的形式去计算的。但也有一些图形API,例如DirectX采用的是行优先的向量表达方式。对于这种表达方式,我们通常会把顶点的坐标放在左手侧,那么整个变换的坐标就会变成这样:
\[T^T(t) = \left[ \matrix{ 1\ &0\ &0\ &0\ \\ 0\ &1\ &0\ &0\ \\ 0\ &0\ &1\ &0\ \\ t_x\ &t_y\ &t_z\ &1\ } \right]\\\\ v' = v·T^T(t)\]实际上无论是行优先还是列优先都没有实际性质上的差异,大部分情况我们都可以直接转置来适配另一种表达方式。这本书会以列优先的表达方式去讲解变换的这一部分。
为平移的矩阵求逆,我们只需要把T(t)写成T(-t),也就是往反方向平移。
4.1.2 旋转
二维空间下实际上我们只能围绕着z轴去进行旋转,矩阵如下:
\[\left[ \matrix{ cosx& -sinx\\ sinx& cosx } \right]\]一个基础的旋转矩阵只能围绕着x,y,z的其中一个轴进行旋转,三维的情况下要分成三个矩阵:
\[R_x(\phi) = \left[ \matrix{ 1 & 0 & 0 & 0\\ 0&cos\phi& -sin\phi&0\\ 0&sin\phi& cos\phi &0\\ 0&0&0&1 } \right]\\\\ R_y(\phi) = \left[ \matrix{ cos\phi & 0 & sin\phi & 0\\ 0 & 1 & 0 & 0\\ -sin\phi & 0 & cos\phi & 0\\ 0 & 0 & 0 & 1 } \right]\\\\ R_z(\phi) = \left[ \matrix{ cos\phi & -sin\phi & 0 & 0\\ sin\phi & cos\phi & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 } \right]\]所有旋转矩阵的行列式都是1,也代表他们为正交。
假设我们想要围绕一个特定的点去旋转,也就是不围绕原点进行旋转,例如我们围绕点p转。那么我们就需要在旋转的前后进行平移的操作。也就是把移动到点p把它当作原点进行旋转,然后再移动回原本的位置:
\[X = T(p)· R(\phi) · T(-p)\\ v' = X·v\]4.1.3 缩放
缩放的矩阵为:
\[S(s) = \left[ \matrix{ s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0\\ 0 & 0 & s_z & 0\\ 0 & 0 & 0 & 1 } \right]\\\\\]逆矩阵为
\[S^{-1}(s) = S(\frac{1}{s_x},\frac{1}{s_y},\frac{1}{s_z} )\]4.1.4 错切(Shearing)
错切是可以用于展现扭曲效果的一个变换。一个基本的错切格式是下面这种:
\[H_{xy}(s) = \left[ \matrix{ 1 & 0 & s & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 } \right]\\\\\]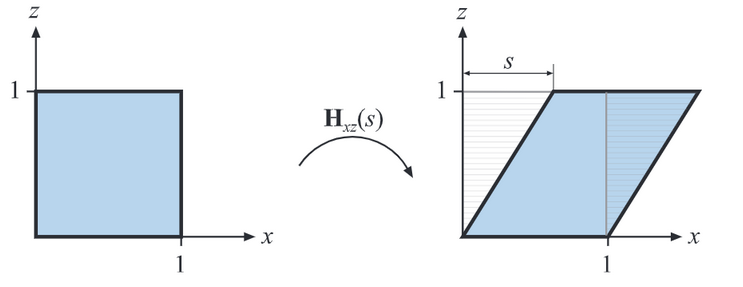
错切到底做了什么?拿Hxy来说, x为唯一移动了的轴。也就是说在Hxy的错切变换里,y/z都是保持静止的。 Hxy的z则是影响x便宜的系数,x的偏移量等于z*S
所以错切本身有六种不同的变换矩阵,分别对应每个轴依赖于另一个轴的错切变换。并且他的逆矩阵也很简单的就是把s的值正负翻转。
4.1.5 连续变换
我们大部分时候都是要对一个物体进行大量的不同的变换。为了提高计算的效率,我们可以把大量不同的变换先提前计算成一个独立的矩阵,这样我们就只需要发送一个矩阵给我们的Shader。
一般来说我们会为一个物体按照顺序的进行缩放,旋转,平移这三个操作。我们可以直接把三个操作合成一个变换矩阵用来操控我们的点:
\[行优先的方式: \\ X = S·R·T\\ v' = v·X\\ v' = v·S·R·T\\\\ 列优先的方式:\\ X = T·R·S\\ v' = X·v\\ v' = T·R·S·v\]很明显的就是我们的变换的顺序是跟哪个离操作的点近来决定的,所以如果我们使用列优先的格式来处理向量,那么我们就需要以TRS的顺序去预先计算我们的变换矩阵,之后在乘以原始坐标的时候就会按照[缩放->旋转->平移]的顺序展开。
4.1.6 法线变换
在我们对一个形状进行变换的时候,我们同时也要对物体的法线进行操作。要知道我们一般进行变换的时候是把平移+旋转+缩放整合成一个矩阵[Model矩阵]传入Shader来控制变换。
\[M_{model} = T·R·S\\ v' = M_{model}·v\]在顶点变换的时候,法线也同时应该变换,比如说顶点转了180度,法线也应该转180度。那么我们理所当然的会想到:
\[N:法线\\ N' = M_{model} · N\\\]不过法线他并不是一个点,而是一个方向,理所当然的不应该享受位移。而位移在整个Model矩阵中处于最右的列和最下的行[齐次坐标出来的维度]。因此我们只需要把这个维度砍掉,让Model矩阵变成一个3x3矩阵,就只剩下旋转和缩放了:
$$
M’{model}: 3x3的Model矩阵
N’ = M’{model} ·N
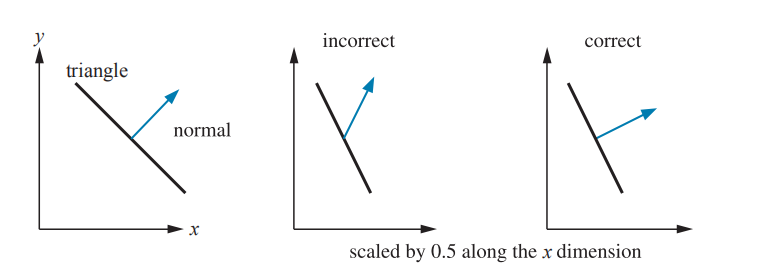
$$ 不过如上图所示,在对称缩放的情况下,其实缩放对法线的影响等同于没有,因为在对称缩放的时候物体是等比例的变大/变小,并不会影响法线的方向。我们需要考虑的是不对称缩放导致个别斜面的斜率变化的情况。如上面的图表示的,如果我们把不对称缩放放到法线上,会出现一个错误的结果。这是因为斜率变换的时候我们不应该把法线跟线往同一个方向拉伸,这会导致方向不正交,应该把法线往反方向拉。
数学的表示反方向拉伸就是缩放矩阵的逆矩阵,这个也很好得到。缩放矩阵的逆矩阵就是:
\[S^{-1}(s) = S(\frac{1}{s_x},\frac{1}{s_y},\frac{1}{s_z} )\]总的来说,如果要让法线成功的变换到正确的方向,需要: 旋转矩阵+缩放逆矩阵
关于逆的转置
书里也提到,网上也有的一个很常见的法线变换的方法是选取Model矩阵左上角的3x3的逆的转置,这个做法本质上就是通过Model矩阵找到正常的旋转和逆的缩放:
\[M : 3x3\ model\ matrix \\ N' = (M^{-1})^T·N\\ M = S·R\\ (M^{-1})^T = (R^{-1}·S^{-1})^T = (S^{-1})^T·(R^{-1})^T\\ S\ is\ Symmetric/Diagonal => S^{-1}\ is\ Symmetrix/Diagonal \\ => (S^{-1})^T = (S^{-1})\\ R\ is\ Orthogonal => (R^{-1})^T = R\\\\ (M^{-1})^T = (S^{-1})·R\]这个做法在特定的情况下是很聪明的,因为我们不需要得到旋转和缩放各自的矩阵,就可以通过一个大的Model矩阵来拆出我们需要的变换。通过逆的转置让顺序不做变换,并且通过缩放和旋转矩阵各自的特性让旋转保持不变,且缩放求逆。
不过在自己的开发当中这样的做法还需要考虑。我们唯一会用到这个传统方法的时候是当我们只传入Model到Shader,不过求逆本身的开销还是比较大的,因为我们的Shader可能并不知道他们的特性,而是会从行列式开始算,这也很有可能导致逆求不出来。
可以的情况下我们完全可以在外部求好:
\[X = (S^{-1})·R\]这样的3x3矩阵传入Shader,可能更有效率一些,只会额外的开销一个3x3矩阵的内存。